【JavaScript】 テキスト差分をWuらによるO(NP)アルゴリズムで算出してみる
更新日:2023/05/15
二つの文字列の相違点を知りたいときUNIX系ならdiffなどのコマンドが使用できます。
しかしWindowsにはそんなコマンドありません。
そこでブラウザでの文字列比較ツールの作成を最終目的として、JavaScriptでのテキスト差分検出を実装してみます。
2023/5/15 コードの一部に誤りがあったので修正しました。
テキスト差分検出の概要
まずはエディットグラフを使用したテキストの差分検出について、簡単に説明します。
SESとか編集距離など難しい概念で解説されることが多いですが、この記事では簡単な言葉で概要をお伝えします。
挿入と削除を繰り返してテキストを加工する
まず短い文字列と、その文字列より長い文字列を用意します。
①JavaScriptかJSか?←短い文字列
②JSはJavascriptのことか?←長い文字列
そして短い文字列に対して文字の挿入や削除といった編集をおこない、長い文字列と同じものを生成します。
| ① | ○ | Java | S | ○ | cript | かJS | ○ | か? |
| ↑ | ↑ | ↑ | ||||||
| ② | JSは | Java | s | cript | のこと | か? | ||
このとき、挿入や削除した文字列が差分となります。
エディットグラフ
差分を考えるときに用いられるのが次のエディットグラフです。
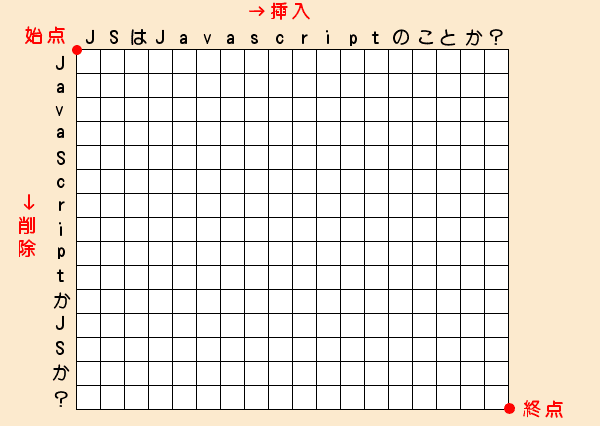
エディットグラフは長い文字を横座標に、短い文字を縦座標に配置します。
そして始点から終点に向かってマス目の辺を移動していきます。
このとき下方に移動したら、短い文字の該当する部分を削除します。
横に移動したら、短い文字に長い文字の該当する部分を挿入します。
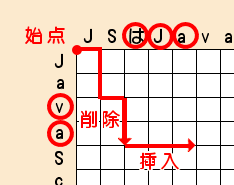
一文字ごとに削除したら一回、挿入したら一回と回数をカウントします。
例は長い方が18文字、短い方が15回なので合計33回編集がおこなわれたことになります。
どんなコースをたどっても、終点に到達した時点で長い文字に置き換わります。
下方移動で短い文字が全部削除されて、横移動で長い文字が全部挿入されるのだから当たり前ですね。
これだけだと『だから何?』という話なので、次はグラフ上で文字が一致する全てのマスに左上から右下に向かって斜線を引きます。

こんどは斜線も通行可能です。
しかも、斜線を通過する場合は編集回数をカウントしません。
この状態で始点から終点までのルートのうち、一番編集回数が少ないものを考えてみます。
一番編集回数が少ないものが、一番効率的な差分データと考えることができます。
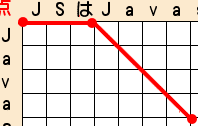
次の図のように11回で到達できます。

このとき通過した斜線部分が、テキストの共通部分となります。
斜線と斜線の間はどのようなルートでも回数は同じですが、一塊の文字列を追加または削除したほうが効率がいいので、できる限り直進しています。
Wu らによる O(NP) アルゴリズム
テキスト差分の検出にはいろいろな手法がありますが、今回はO(NP)のアルゴリズム(An O(NP) Sequence Comparison Algorithm)を用いて実装していきます。
このアルゴリズムは、上記の差分探索を効率よく行うことを目的としたアルゴリズムです。
An O(NP) sequence comparison algorithmでの概要 の要約
文字列AとBの長さをMとNとしてN>=Mが成り立つ時、Dを挿入と削除の長さとします。 Dに関連するパラメータは削除数です。 アルゴリズムで導き出される最短編集距離は最大実行時間がO(NP)で、予想実行時間がO(N + PD)です。AがBが似た文字列の場合は非常に効率的です。これは、マイヤーズのO(ND)アルゴリズムのほぼ2倍の速度であり、AとBの長さが大幅に異なる場合ははるかに効率的です。
ここではアルゴリズムについて解説していきます。
JavaScriptのコード
次のコードは、WuらによるO(NP)のアルゴリズムの論文に掲載されているコードをJavaScriptにしたものです。
const max = Math.max;
const AlgorithmCompare = () =>{
const fp = [];
for( let i = -(M+1) ; i <= N+1 ; i ++ ) fp[i] = -1;
let p = -1;
do{
p ++;
for( let k = -p ; k <= Δ -1 ; k ++ ) // ループ1
fp[ k ] = snake( k, max( fp[ k - 1 ] + 1, fp[ k + 1 ] ) );
for( let k = Δ + p ; k >= Δ + 1 ; k -- ) // ループ2
fp[ k ] = snake( k, max( fp[ k - 1 ] + 1, fp[ k + 1 ] ) );
fp[ Δ ] = snake( Δ, max( fp[ Δ - 1 ] + 1, fp[ Δ + 1 ] ) ); // Δの処理
}while( fp[Δ] !== N );
return Δ + 2 * p;
};
const snake = ( k , y ) =>{
let x = y - k;
while ( x < M && y < N && A[ x ] === B[ y ] ){
x ++;y ++;
}
return y;
};
このコードは差分を求めるものではなくて、編集回数を求めることを目的としたものです。
『JavaScriptかJSか?』と『JSはJavascriptのことか?』で実行すると11が返ります。
差分を求めるには、snake関数で一致した文字を記憶しておく処理を追加する必要があります。
具体的な方法は最終的なコードでお伝えします。
コードの前提条件
このコードは前提条件として、次の変数が用意されているとします。
A:短い方のテキスト
B:長い方のテキスト
M:短い方のテキストの文字数
N:長い方のテキストの文字数
Δ:二つのテキストの文字数差(変数N - 変数M)
text1とtext2から各変数を求めるとき、次のようなコードが考えられます。
const [A,B] = text1.length < text2.length ? [text1,text2] : [text2,text1];
const [M,N] = [A.length , B.length];
const Δ = N - M;
JavaScriptの変数はユニコードを受け付けるので漢字などの2バイトコードを使用できます。
そのため原文で使用しているΔ(デルタ)をそのまま変数で使用しています。
■参考記事:【JavaScript】 文字列データの内部形式と関連メソッドについてまとめてみた
配列fpの添え字でマイナスを使用していますが、JavaScriptの配列はマイナス値を配列インデックスとして認識しません。
しかし配列もオブジェクトなので、fp.abcなどのプロパティ名と同じ扱いで登録されています。
ここからは次の条件で解説を進めます。
A:"ABcDe"
B:"AB12D34"
M:5
N:7
Δ:2
エディットグラフと配列fp
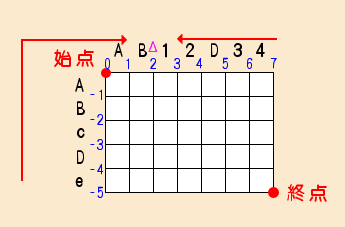
変数Bを横軸、変数Aを縦軸にしてエディットグラフを書きます。
このとき、始点から横方向にプラス、下方向にマイナスでマスの罫線ごとに番号を振っていきます。

AlgorithmCompare関数の配列fpはこの番号に対応していて、初期化後の状態は次のようになっています。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
関数snakeの処理内容
関数snakeの引数kは、エディットフラグに振った番号です。
引数yは長い方の文字位置で、変数xは短い方の文字位置です。
計算上は、x = y - kで求められます。
変数xを求めるには、まず各文字をエディットグラフ上の罫線上に配置します。
次にkから斜めに線を引きます。
yに対応する文字から下方に向かって引いた直線線を引き斜め線と交差したら左方向へ線を引きます。
現れた文字の位置が変数xの値です。
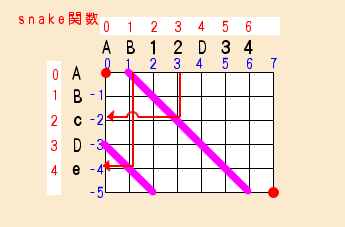
k = 1 , y = 3 のとき、xは2です。
k = -3 , y = 1 のとき、xは4です。
関数snakeは A[ x ] と B[ y ] を比較して同じならxとyを一つ進め次の文字を比較します。
そして一致しない時点で y 値を返します。
つまり、一致しなかった文字の位置を返します。
例:AB1とABcのとき、3番目に相当するy値が返る
AlgorithmComparesnakeの処理内容
AlgorithmCompare関数のdoループは二つのループで構成されています。
最初のループ(ループ1)は、番号の小さいものからΔの直前まで一つづつ増やしていくループです。
一回目のループは0から開始しますが、2回目以降は-1,-2と開始位置が外側に広がっていきます。
次のループ(ループ2)は、番号の大きいものからΔの直前まで一つづつ減らしていくループです。
一回目のループは処理されませんが、2回目以降は開始位置が一つづつ増えていきます。
では、実際の処理を追ってみます。
配列fpの値および、Δの位置は次のようになっています。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
まずは最初のループです。
●p = 0 , k = 0 のとき
max( fp[ k:0 - 1 ] + 1, fp[ k:0 + 1 ] ) は max( -1 + 1 , -1 ) で 0 です。
関数snakeは、A[ x:0 ]と B[ y:0 ]から文字のマッチングを処理します。
A[ x:0 ]と B[ y:0 ] が一致
A[ x:1 ]と B[ y:1 ] が一致
A[ x:2 ]と B[ y:2 ] が一致しない
今回のテキストは最初の二文字が一致しました。
関数snakeは、一致しなかった文字Bの位置、すなわち2が返ってきます。

fp[ k:0 ] に返ってきた値2をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | -1 | 2 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
| k |
●p = 0 , k = 1 のとき
最初のforループでkを一つ進めます。
fp[ k:1 - 1 ]は、直前のループで処理されて2がセットされています。
そのため、max( fp[ k:1 - 1 ] + 1, fp[ k:1 + 1 ] ) は 3 です。
x は y:3 - k:1 で2です。
関数snakeは、A[ x:2 ] , B[ y:3 ] から文字のマッチングを処理します。
この位置はマッチしないので、yがそのまま帰ってきます。
今回の処理ではマッチングがありませんでした。
とりあえずk=0のときとの関連性を示すため、比較を行った文字間で線を引いておきます。
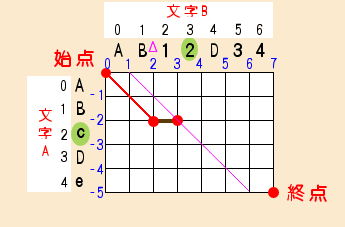
fp[ k:1 ] に返ってきた値3をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | -1 | 2 | 3 | -1 | -1 | -1 | -1 | -1 | -1 |
| k |
Δの値は2です。
最初のループはΔの直前までなので、これで終了です。
ループ2は、一回目のdoループでは処理されません。
●p = 0 ,k=Δ=2の処理
doループの最後はΔの処理を行います。
Δの値は2なので、max( fp[ Δ:2 - 1 ] + 1, fp[ Δ:2 + 1 ] ) でmax( 3 + 1, -1 ) となって、yの値は4です。
そしてxは y:4 - Δ:2で、前回と変わらず2です。
A[ x:2 ]とB[ y:4 ]はマッチしないので、関数snakeの結果は4です。
図の方も前回と同じように線を引いておきます。
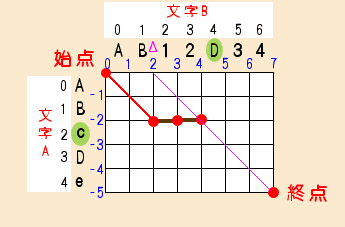
そして、fp[ Δ:2 ] に返ってきた値4をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | -1 | 2 | 3 | 4 | -1 | -1 | -1 | -1 | -1 |
| Δ |
●p = 1 , k = -1 のとき
2回目のdoループは、pがインクリメントされます。
そのためループ1は、k=-1からスタートします。
とはいえ、これまでとやることは同じです。
max( fp[ k:-1 - 1 ] + 1, fp[ k:-1 + 1 ] ) は 、max( -1 + 1, 2 ) で 2 です。
xは y:2 - ( k:-1) で3です。
A[ x:3 ] とB[ y:2 ]はマッチしないので、関数snakeの結果は2です。
今回も図に線を入れておきます。
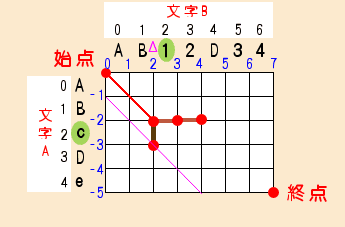
経路が二つに分かれましたね。
どうやら2回目のループは新しい経路を探索するようです。
fp[ k:-1 ] に返ってきた値2をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | 2 | 2 | 3 | 4 | -1 | -1 | -1 | -1 | -1 |
| k |
●p = 1 , k = 0 のとき
ここまでくると少し様子が変わってきます。
なんとfp[ k:0 ] の前後に値が入っています。
編集処理を早く終わらせるには、現時点で文字列Bのマッチが進んでいる方を選択するのがよさそうです。
ということで、max( fp[ k:0 - 1 ] + 1, fp[ k:0 + 1 ] ) の式で値が大きい方を取得しているのです。
max( fp[ k:0 - 1 ] + 1, fp[ k:0 + 1 ] ) はmax( 2 + 1, 3 ) で3です。
そして x は y:3 - k:0 で3です。
A[ x:3 ] とB[ y:3 ]はマッチしないので、関数snakeの結果は3です。
今回も図に線を引きたいのですが、経路が二つに分かれているのでどちらを選択するか迷いますね。
とりあえずmax( ・・・ )を見ると、最初の引数に+1をしているので、そちらを優先するような意思を感じます。
そこで-1側を選択します。

そしてfp[ k:0 ] に3をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | 2 | 3 | 3 | 4 | -1 | -1 | -1 | -1 | -1 |
| k |
●p = 1 , k = 1 のとき
ここも同じように処理します。
一文字一致するので、snake関数の結果は5になります。

fp[ k:1 ] に5をセットします。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | 2 | 3 | 5 | 4 | -1 | -1 | -1 | -1 | -1 |
| k |
●p = 1 , k = 3(Δ+1) のとき
ここで初めてループ2が実行されます。
ですが、やることは同じです。
max( fp[ k:3 - 1 ] + 1, fp[ k:3 + 1 ] ) はmax( 4 + 1, -1 ) で5です。
xは y:5 - k:3 で2です。
文字が一致しないので、snake関数の結果は5になります。
図にすると次のようになります。

fpの参照先がインデックス2なので、そちらの分岐と接続しています。
このようにdoループが回るごとに新しい可能性を探っていくことになります。
| Δ | |||||||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| fp | -1 | -1 | -1 | -1 | 2 | 3 | 5 | 4 | 5 | -1 | -1 | -1 | -1 |
| k |
●p = 1 ,k=Δ=2の処理
2回目のΔの処理もこれまでと同じです。
処理結果を図にすると次のようになります。
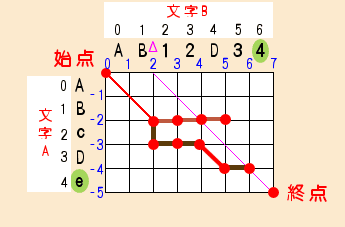
この後p値を増加させてループ処理を続けていくと、Δの処理の終了時に、次の図のようにエディットグラフの終点に到達します。

この時点で編集作業の探索が終了します。
それをチェックしているのが、次のコードです。
while( fp[Δ] !== N );
その時点でのp値を2倍してΔを加算した値が、編集回数になります。
差分を求める方法
ここまで紹介したアルゴリズムで編集回数を求めることができましたが、求めたいのはテキストの差分です。
そこで、その方法について解説してみます。
一致した情報を記憶する
差分を求めるには、snake関数内で文字が一致したときに、その情報を記憶しておきます。
さらに一致した情報どうしのつながりを保持する仕組みを構築して、k値を元に取り出せるようにします。
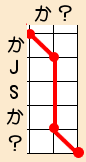
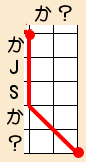
例えば次の図のように、赤線の部分が一致するテキストがあるとします。
アルゴリズムを適用した結果、赤線の部分が共通テキストとして情報が登録されているとします。

このとき、k値2(Δ)から②の情報を取得し、さらに②から①を取得できるような仕組みです。
つまり後ろから前へと追っていく形になります。
挿入と削除については、図を見てもらうとわかりますが、共通データ同士の始点と終点を接続させるように文字を選択するだけです。
一致した情報を記憶するコード
最初のアルゴリズムを、できるだけ原型を留めるようにして、差分情報を取得できるようにしたのが次のコードです。
const fp = [];
const path = [];
const AlgorithmCompare = () =>{
for( let i = -(M+1) ; i <= N+1 ; i ++ ) fp[i] = {y:-1,previous:-1};
path.length = 0;
let p = -1;
do{
p ++;
for( let k = -p ; k <= Δ -1 ; k ++ )
fp[ k ].y = snake( k, max( fp[ k - 1 ].y + 1, fp[ k + 1 ].y ) );
for( let k = Δ + p ; k >= Δ + 1 ; k -- )
fp[ k ].y = snake( k, max( fp[ k - 1 ].y + 1, fp[ k + 1 ].y ) );
fp[ Δ ].y = snake( Δ, max( fp[ Δ - 1 ].y + 1, fp[ Δ + 1 ].y ) );
}while( fp[Δ].y !== N );
return getSes( );
};
const snake = ( k , y ) =>{
let x = y - k;
const [sx,sy] = [x,y];
while ( x < M && y < N && A[ x ] === B[ y ] ){
x ++;y ++;
}
const leftOrRight = fp[ k - 1 ].y + 1 >= fp[ k + 1 ].y ? -1 : 1;
const previous = fp[ k + leftOrRight ].previous;
if( sx !== x ){
fp[ k ].previous = path.length;
path.push( { endX : x-1 , endY : y -1 , length : x - sx ,previous:previous });
}else{
fp[ k ].previous = previous;
}
return y;
};
const DELETE = Symbol();
const INSERT = Symbol();
const COMMON = Symbol();
const getSes = () =>{
const result = [];
let [cX,cY] = [M-1,N-1];
let [sX,sY] = [-1,-1];
let previous = fp[ Δ ].previous;
while (previous !== -1) {
const {endX,endY,length} = path[ previous ];
[sX,sY] = [endX - length +1,endY - length +1];
if( cX !== endX ) result.push( {s:endX +1 , e:cX , flg:DELETE });
if( cY !== endY ) result.push( {s:endY +1 , e:cY , flg:INSERT });
result.push( {s:sX , e:endX , flg:COMMON });
[cX,cY] = [sX-1,sY-1];
previous = path[ previous ].previous;
}
if( sX !== 0) result.push( {s:0 , e:cX , flg:DELETE });
if( sY !== 0) result.push( {s:0 , e:cY , flg:INSERT });
result.reverse()
return result;
}
2023/5/15 コードの一部に誤りがあったので修正しました。
下から5行目: e:sX → e:cX、下から6行目: e:sY → e:cY
取得した経路情報の内容
配列pathには、次のような共通データ情報が登録されます。
{ endX : 終点x , endY :終点y , length : 長さ , previous: 共通データへのインデックス }
始点は終点と長さから計算可能です。
さらに配列fpに、これまでのデータに加え、共通データ情報へのインデックスを登録できるようにしてあります。
このコードに次のテキストを適用してみます。
text1 : "JavaScriptかJSか?"; text2 : "JSはJavascriptのことか?";
すると、次のような結果が返ってきます。
[
{ s: 0, e: 0, flg: Symbol(COMMON) },
{ s: 1, e: 3, flg: Symbol(INSERT) },
{ s: 1, e: 3, flg: Symbol(COMMON) },
{ s: 7, e: 7, flg: Symbol(INSERT) },
{ s: 4, e: 4, flg: Symbol(DELETE) },
{ s: 5, e: 9, flg: Symbol(COMMON) },
{ s: 13, e: 15, flg: Symbol(INSERT) },
{ s: 10, e: 10, flg: Symbol(COMMON) },
{ s: 11, e: 13, flg: Symbol(DELETE) },
{ s: 14, e: 14, flg: Symbol(COMMON) }
]
この結果から、次のようなコードで可視化できます。
const printSes = algorithmCompareResult => algorithmCompareResult.forEach( e=>{
const data = {
[DELETE] :{pre:"-",text:text1},
[INSERT] :{pre:"+",text:text2},
[COMMON] :{pre:" ",text:text1}
}[ e.flg ];
console.log( data.pre + data.text.substring( e.s,e.e+1) );
});
printSes( AlgorithmCompare() );
次のように表示されます。
J +SはJ ava +s -S cript +のこと か -JSか ?
"+"が挿入で"-"が削除を、" "が共通データを表しています。
これをエディットグラフにすると、次のようになります。
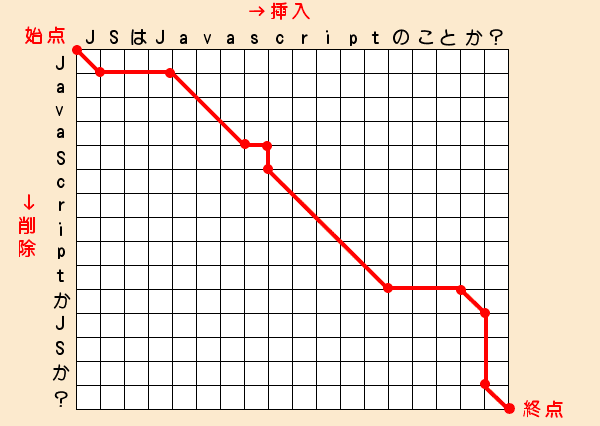
これでテキスト差分を求めることができました。
想定したものと異なる結果となることもある
実は概要で挙げたものとは異なる結果だったりします。
概要で挙げたのは、次のようなものでした。

今回のアルゴリズムは、先頭で一致するとその時点で共通データとして処理されてしまうので、こうなるのが当たり前だったりします。
ちょっと残念です。
エディットグラフでの差分検出は、挿入と削除の回数が最小限となるように経路を算出します。
上記の二つの経路は、ともに挿入7回削除4回なので、どちらも正解です。
差分データを加工する
前項のアルゴリズムで取得した編集データは、テキスト差分検出の概要に提示したものと異なるものとなってしまいました。
この結果は十分に実用的なものだと思いますが、せっかくの機会なので概要の結果に近づけてみます。
アルゴリズムを変更すると汎用性が著しく損なわれるので、編集データを加工してみます。
実は、編集データには次のような特徴があります。
データが、『共通、挿入、共通』または『共通、削除、共通』の順番に並んでいて、最初の文字列と2番目の文字列の末尾が一致するとき、
最初の文字列の末尾を2番目の文字列の先頭に移動して、2番目の文字列の末尾を3番目の文字列の先頭に移動できる。
ようするに、次のように移動できます。
| 移動前 | 移動後 | |||||
|---|---|---|---|---|---|---|
| 挿入 | SはJ | JSは | ||||
| 共通 | J | avas | ⇒ | Javas | ||
| 削除 | ||||||
|
| |||||
| 移動前 | 移動後 | |||||
|---|---|---|---|---|---|---|
| 挿入 | ||||||
| 共通 | か | ? | ⇒ | か? | ||
| 削除 | JSか | かJS | ||||
|
| |||||
この処理をおこなうと、理想の形とほぼ同じになります。
そして次のコードは、共通部分が一文字で、後に続く挿入または削除の最後の文字が共通部分と同じ時に、文字の入れ替えをおこなっています。
const getText = r => ({
[DELETE] :text1,
[INSERT] :text2,
[COMMON] :text1
}[ r.flg ]).substring( r.s,r.e+1)
const processingSes = AlgorithmCompareResult => AlgorithmCompareResult.reduce(
(a ,b , index )=>{
if( a.insertChar !== null ){
if( b.flg !== COMMON) a.data.push( { s:b.s - 1, e:b.e-1 , flg:b.flg} );
else {
a.data.push( { s:b.s - 1, e:b.e , flg:b.flg} );
a.insertChar = null;
}
return a;
}
if( b.flg === COMMON && b.s === b.e ){
const next1 = AlgorithmCompareResult[index+1];
const next2 = AlgorithmCompareResult[index+2];
if( next1 !== undefined && next2 !== undefined &&
next1.flg !== COMMON && next2.flg === COMMON){
const [t1,t2] = [ getText( b ) , getText( next1 )];
if( t2.endsWith(t1) ) {
a.insertChar = t1;return a;
}
}
}
a.data.push( b );
return a;
},{ insertChar:null,data:[]}).data;
printSes( processingSes( result ) );
結果は次のようになります。
+JSは Java +s -S cript +のこと -かJS か?
想定した結果になりました。
このコードはあくまで今回例示した文字列に対応させたものです。
そのため、実用的なものではありません。
実用的なものにするなら、共通文字列が最小になるようなアルゴリズムを組む必要があると思います。
考え方は難しくないと思います。
後方だけでなく前方にも振り分けられるかチェックして、文字列全体が振り分けられるようなら振り分けます。

コードが長くなりそうなので、ここではやりません。
タグを考慮した差分
加工のアイデアとしてタグ単位での差分を作成してみます。
例えば次のような二つのhtmlタグがあるとします。
タグ1:<div><p>テスト</p></div>
タグ2:<div><p id=\"id1\">テスト</p></div>
この二つの文字列の差分を求めると、次のようになります。
<div><p + id="id1" >テスト</p></div>
これを、次のようにタグ単位で差分検出してみようと思います。
<div> -<p> +<p id="id1"> テスト</p></div>
考え方は簡単です。
共通部分に閉じられていないタグがあったらその開始位置を保存して、閉じタグを検出したら開始から終了までの編集データを再構成します。
const getText = r => ({
[DELETE] :text1,
[INSERT] :text2,
[COMMON] :text1
}[ r.flg ]).substring( r.s,r.e+1)
const processingSesTag = AlgorithmCompareResult =>{
const workObj = {cp1:0,cp2:0, // 現在の文字位置
ltPos:{index:-1,position:0,tp1:0,tp2:0}, // 開始タグ"<"の位置
result:[],
cp1Add:function (b){ this.cp1 += b.e - b.s + 1;return this;}, // text1の文字位置を進める
cp2Add:function (b){ this.cp2 += b.e - b.s + 1;return this;}, // text2の文字位置を進める
cpAdd:function (b){ return this.cp1Add(b).cp2Add(b);}
};
return AlgorithmCompareResult.reduce(
(a,b)=>{
const result = a.result;
result.push( b );
switch ( b.flg ){
case DELETE:return a.cp1Add(b);
case INSERT:return a.cp2Add(b);
case COMMON:break;
default:throw new TypeError("入力データ不正");
}
const ltPos = a.ltPos;
const b2 = ltPos.index === -1 ? b : (()=>{
// ">"が最初に現れるとき、閉じタグとみなす
const text = getText(b);
const [lt,gt] = [text.indexOf("<"),text.indexOf(">")];
if( gt >= lt ) return b;
const {index,position,tp1,tp2} = ltPos;
// 編集データを再構成する
const w = result[index];
result.length = index;
if( position > 0 ) result.push( {s:w.s,e:w.s+position-1,flg:COMMON} );
result.push( {s:tp1 + position,e:a.cp1+gt,flg:DELETE}
, {s:tp2 + position,e:a.cp2+gt,flg:INSERT} );
const afterCOMMON = text.length === gt + 1 ? null :
{ s:b.s + gt + 1,e:b.e,flg:COMMON};
if( afterCOMMON !== null ) result.push( afterCOMMON );
ltPos.index = -1;
return afterCOMMON;
})();
if( b2 === null ) return a.cpAdd(b);
// 文字列に閉じられていないタグがあるか確認
const text = getText(b2);
const [lt,gt] = [text.lastIndexOf("<"),text.lastIndexOf(">")];
if( lt > gt ){ // タグ開始位置保存
ltPos.index = result.length -1;
ltPos.position = lt;ltPos.tp1 = a.cp1;ltPos.tp2 = a.cp2;
}
return a.cpAdd(b);
},workObj
).result;
};
const text1 = "<div><p>テスト</p></div>";
const text2 = "<div><p id=\"id1\">テスト</p></div>";
printSes( processingSesTag( AlgorithmCompare() ) );
これで、上記のような結果になります。
ただし、このコードは例として挙げたタグでのみテストをしています。
そのため、他のタグでは上手く動作しない可能性があります。
あくまで例として参考にしてください。
JavaScriptソースコード
ここまでに例示したコードは論文で例示されていたコードを可能な限り変更しないようにJavaScript化したため、Arrayオブジェクトにマイナスインデックスをプロパティ名として強引に付加しています。
そこでマイナスインデックスを使用しないような方法でJavaScriptで関数化してみます。
考え方は、k値をマイナス側から配列に割り振ります。
| 配列インデックス | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| fp | -1 | -1 | -1 | -1 | 2 | 3 | 5 | 4 | 5 | -1 | -1 | -1 | -1 |
| k値 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
そして、k値が0となる配列インデックスをオフセットとします。
上の例では、k値が0になるのはインデックス5なので、オフセットは5です。
オフセット = 5
配列にアクセスするときは、オフセットにk値を加算することで配列のインデックスを求めることができます。
k値0のとき、インデックス5
k値-3のとき、インデックス2
k値4のとき、インデックス9
今回は配列(Arrayオブジェクト)ではなくてArrayBufferを使用してみました。
配列のインデックスはプロパティなので、アクセスするたびにプロパティの検索がおこなわれます。
ArrayBufferは、単純な計算でアクセス先が算出されます。
ArrayBufferの方が速い気がしますね。
ArrayBufferについてはこちらを読んでみてください。
■【JavaScript】 ArrayBufferとTypedArray-メモリを確保してアクセス
なお、コード上では32ビットの整数値でArrayBufferを初期化しています。
そのため理論上の文字列の最大長は32ビットの整数値の最大値になると思います。
ここでは文字列の長さチェックをしていませんが、速度を考えると、もっと少ないサイズで制限を入れた方がいいかもしれません。
また、アルゴリズムは二つの文字列の長さの大小が、いつも同じ関係になる必要があります。
関数を呼び出すときに毎回チェックするのは非効率なので、関数内でチェックするようにしました。
const onp = (()=>{
const TEXT_SWAPPED = true;
const DELETE = 1;
const INSERT = 2;
const COMMON = 0;
const onp = ( text1 , text2 ) => {
const onpFUnc = {
exec : function( text1 , text2 ){
return this.initOnp( text1 , text2 ).onpMain().getSes();
},
initOnp :function (text1,text2) { // 初期化
const allocBuff = (size,intVal) =>(new Int32Array(size)).fill(intVal);
const [M,N] = [text1.length,text2.length];
const data = M > N ? {textX:text2,textY:text1,M:N,N:M,swappedFlg:TEXT_SWAPPED}
: {textX:text1,textY:text2,M:M,N:N,swappedFlg:!TEXT_SWAPPED};
const flg = data.swappedFlg ? { ses_insert:DELETE,ses_delete:INSERT , commonType:onp.flg.TEXT2}
: { ses_insert:INSERT,ses_delete:DELETE , commonType:onp.flg.TEXT1}
const size = M + N + 3;
this.onpData = {
fp:allocBuff(size,-1) ,
pathRef:allocBuff(size,-1) ,
path:[],
offset : data.M + 1,
delta : data.N - data.M,
data : data,
flg : flg
};
return this;
},
onpMain : function(){
const { fp , pathRef , path , offset , delta } = this.onpData;
const { textX , textY , M , N } = this.onpData.data;
const snake = ( k ) => {
const kOffset = k + offset;
const kOffsetMinus = kOffset -1;
const kOffsetPlus = kOffset +1;
const p1 = fp[kOffsetMinus]+1;
const p2 = fp[kOffsetPlus];
let [previous,py] = p1 > p2 ? [pathRef[kOffsetMinus], p1]
:[ pathRef[kOffsetPlus] ,p2]
let px = py - k;
const sx = px;
while (px < M && py < N && textX[px] === textY[py]) {
px++;py++;
}
if( sx !== px ){
pathRef[kOffset] = path.length;
path.push( {endX:px-1, endY:py-1 , length:px-sx ,previous:previous } );
}else{
pathRef[kOffset] = previous;
}
fp[kOffset] = py;
return py;
};
let k,P;
for (P = 0; P <= M; P++) {
for ( k = -P; k < delta; k++) snake(k);
for ( k = delta + P; k > delta; k--) snake(k);
if( snake(delta) === N ) break;
}
this.onpData.fp = null; // 参照オフ(気休め)
return this;
},
getSes:function (){
const epcData = [];
const { pathRef , path ,delta , offset } = this.onpData;
const { M , N } = this.onpData.data;
const { ses_insert , ses_delete } = this.onpData.flg;
const ses_common = COMMON;
let [cX,cY] = [M-1,N-1];
let [sX,sY] = [-1,-1];
let previous = pathRef[delta+offset];
while (previous !== -1) {
let epc = path[previous];
const {endX,endY,length} = epc;
[sX,sY] = [endX - length +1,endY - length +1];
if( cX !== endX ) epcData.push( {s:endX +1 , e:cX , flg:ses_delete });
if( cY !== endY ) epcData.push( {s:endY +1 , e:cY , flg:ses_insert });
epcData.push( {s:sX , e:endX , flg:ses_common });
[cX,cY,previous] = [sX-1,sY-1,epc.previous];
}
if( sX !== 0) epcData.push( {s:0 , e:sX , flg:ses_delete });
if( sY !== 0) epcData.push( {s:0 , e:sY , flg:ses_insert });
epcData.reverse()
this.onpData.pathRef = this.onpData.path = null; // 参照オフ(気休め)
return {commonType:this.onpData.flg.commonType ,data:epcData};
}
};
return onpFUnc.exec( text1 , text2 ) ;
};
Object.defineProperty( onp ,"flg" , {
writable:false,
value:Object.freeze( {
TEXT1 : DELETE,
TEXT2 : INSERT,
COMMON : COMMON
})
});
return onp;
})();
2023/5/15 コードの一部に誤りがあったので修正しました。
下から20行目: e:sX → e:cX、下から21行目: e:sY → e:cY
上のコードを実行すると、関数onp( 文字列1 , 文字列2 )が生成されます。
この関数を実行すると、次のオブジェクトが返ります。
{commonType:共通テキスト ,data:編集データ}
commonTypeは、引数とした与えた文字列のどちらを共通テキストとして使用するかを示すフラグです。
commonType === onp.flg.TEXT1 のとき、文字列1を共通テキストとして使用
commonType === onp.flg.TEXT2 のとき、文字列2を共通テキストとして使用
次のようなコードで、差分を可視化できます。
const text1 = "JavaScriptかJSか?";
const text2 = "JSはJavascriptのことか?";
const result = onp( text1 , text2 );
const commonText = result.commonType === onp.flg.TEXT2 ? text2 : text1;
result.data.forEach( e=>{
switch (e.flg){
case onp.flg.TEXT2:
console.log( "+" + text2.substring(e.s,e.e+1) );
return;
case onp.flg.TEXT1:
console.log( "-" + text1.substring(e.s,e.e+1) );
return
case onp.flg.COMMON:
console.log( " " + commonText.substring(e.s,e.e+1) );
break;
}
});
このコードを元にして、作成したのが次のツールです。

このツールでは、最初に入力文字列を改行で分割して行単位で比較しています。
これにより、行で一致していることを視覚的に提示できるようになっています。
行での差分比較後は、一致しなかった文字列を文字ごとに比較しています。
更新日:2023/05/15
関連記事
スポンサーリンク
記事の内容について

こんにちはけーちゃんです。
説明するのって難しいですね。
「なんか言ってることおかしくない?」
たぶん、こんなご意見あると思います。
裏付けを取りながら記事を作成していますが、僕の勘違いだったり、そもそも情報源の内容が間違えていたりで、正確でないことが多いと思います。
そんなときは、ご意見もらえたら嬉しいです。
掲載コードについては事前に動作確認をしていますが、貼り付け後に体裁を整えるなどをした結果動作しないものになっていることがあります。
生暖かい視線でスルーするか、ご指摘ください。
ご意見、ご指摘はこちら。
https://note.affi-sapo-sv.com/info.php
このサイトは、リンクフリーです。大歓迎です。